

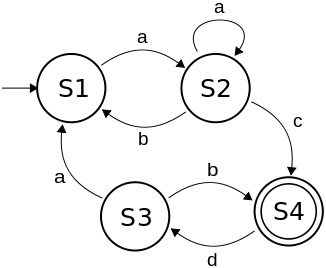
(For an explanation ofįigure 1: A Finite Automaton (FA) for a*ba* The start state is marked by a special short arrow that comes from nowhere, and the final states are marked by double circles. Every transition is marked by a symbol from Otherwise the string is rejected.įor an animation of a finite automaton, please visit this website.įollowing manner: The machine’s states are represented by circles and If this process ends with the machine in an accept state, we say that the Machine reads a letter and makes a transition over and over until the stringĮnds. Is read left to right one character at a time. F can be empty that is, there may not be any final state in an FA as indicated in component-5 of the above definition.įor a simple example of an FA or DFA, please visit this website. Please note that the alphabet does not include the ^ symbol (which stands for the null string). The component-3 of the above definition implies that there is one outgoing transition from ever state for every symbol of the alphabet (sigma). F is a set of final states (or accept states).
: A finite set of symbols, called the alphabet.ĥ. The terms Finite Automata(FA) and Deterministic Finite Automata (DFA) are used interchangeably.Ģ. The word finite refers to the fact that the Of the term final state, other equivalent terms such as terminalĬalled a finite automaton. There are two possible states the switch can be Cohen (1997) Introduction to Computer Theory, 2nd Edition, John Wiley & Sons ) Sipser (2012) Introduction to the Theory of Computation, 3rd Edition, Cengage Learning, and D. Introduction to Automata Theory, Languages, and Computation, 3rd Edition, Addison Wesley., C 0 yields or leads to C n if C 0 ⊢ M* C n.Finite Automata (FA) and Regular Expressions (Based on Define ⊢ M * to be the reflexive, transitive closure of the relation ⊢ M. Let M be a DFA with next move relation ⊢ M. We would like to discuss computations of varying lengths including length zero. The relation ⊢ M was defined to aid in assisting with the descriptions of computations. That is, the DFA is in a configuration C h = ( q, ) ∈ C( M) with the property that p =| x| + 1. If the DFA halts when there is no more input left to process, that is, it is in a configuration C = ( q, τ F( x)) then we say that the DFA is in a final configuration. A halting configuration of a DFA is a configuration C h = ( q, ) ∈ C( M) with the property that δ ( q, σ ) is undefined. This can occur whenever the state transition function is undefined. We say the DFA halts when there is no next state or when the machine moves off the end of the tape.
#Finite state automata generator plus
The tape alphabet Σ T is the set of all possible symbols that appear on the tape, and so it is Σ plus ( by transition 3 ) ⊢ M ( q 2, ) ( by transition 2 ) ⊢ M ( q 2, ) ( by transition 6 ) End markers are not allowed as data symbols for obvious reasons. These are the symbols that can occur on the input tape between 〈 and 〉. Since q 0 ∈ Q, it follows that Q is nonempty however, we prefer to write this condition explicitly in the definition.
Typically, we represent individual states by the symbols q 0, q 1, and so on, but keep in mind that other names would work as well. Let's examine each component of this definition in turn. The M stands for “machine.” We will usually use the symbols M, M', M 1, and so on to denote a machine. Q 0- the initial state or start state, q 0 ∈ Q 5.


 0 kommentar(er)
0 kommentar(er)
